电子电路是由电阻、电感、电容等无源元件,晶体二极管、晶体三极管、场效应管、负阻器件、集成运算放大器等有源电子器件,以及电压源、电流源、受控源等电源元器件组成的电路。无源器件和电源器件一般视为线性器件。电子器件由其工作状态不同分为线性器件和非线性器件;当工作在小信号条件下,等效为线性器件,当工作在大信号或开关状态下,等效为非线性器件。不含非线性器件的电路是线性电路,含一个以上非线性器件的电路是非线性电路。当电路工作频率较低,即波长 远大于电路尺寸
远大于电路尺寸 时,电路是集总参数电路。当
时,电路是集总参数电路。当 与
与 可比拟时,表征电路特性的参数已不能只用一种常规定义下的物理量来表征,而要用无限多个连续分布的基本电路参数来表征,这种元件称为分布参数元件,由分布元件组成的电路是分布参数电路。在
可比拟时,表征电路特性的参数已不能只用一种常规定义下的物理量来表征,而要用无限多个连续分布的基本电路参数来表征,这种元件称为分布参数元件,由分布元件组成的电路是分布参数电路。在 的情况下,表征电路特性的参数已不是电压和电流,而是电场强度和磁场强度,这种电路是微波电路。当电路中的信号是连续时间信号时,电路称为模拟电路;当信号是离散时间信号时,电路称为离散时间电路;当信号是二值化(0,1两个状态)信号时,电路是数字电路。特性或参数随时间变化的元件称为时变元件,含时变元件的电路是时变电路;否则分别称为时不变元件和时不变电路。
的情况下,表征电路特性的参数已不是电压和电流,而是电场强度和磁场强度,这种电路是微波电路。当电路中的信号是连续时间信号时,电路称为模拟电路;当信号是离散时间信号时,电路称为离散时间电路;当信号是二值化(0,1两个状态)信号时,电路是数字电路。特性或参数随时间变化的元件称为时变元件,含时变元件的电路是时变电路;否则分别称为时不变元件和时不变电路。
电路分析通常用基尔霍夫定律列出电路拓扑方程,还要根据元件特性列出元器件约束方程,联合求解电路方程。电路方程包括代数方程、微分方程和差分方程等。针对不同电路和不同激励,有不同的电路分析理论。19世纪以来,对于集总参数时不变线性电路,已有成熟通用的分析理论。而非线性电路还缺少通用理论,但对某些非线性电路,在特定条件下,有近似分析方法研究一些重要的非线性现象。对于分布参数电路,已有用电路的方法分析传输线的理论,时变电路还缺少有效的求解方法。
电子器件与其他电子元件组合,构成功能不同的各种电路。为了分析这些电路,必须把电子器件表示成由某些电路元件组成的简单等效电路。它们可是无源电子元件,也可是受控电流源或受控电压源。尽管等效电路只能近似地反映电子器件的外部特性,但在分析和设计电子电路时却有着十分重要的作用。
通常,按信号幅度的大小,可将电子器件等效电路分为两类:小信号等效电路和大信号等效电路。二极管交流小信号可等效为电阻与电容的并联;晶体三极管和场效应管等效为双端口网络,其中 参量、
参量、 参量、
参量、 参量和
参量和 参量4种参数的等效电路较为常用。高频工作情况下,混合
参量4种参数的等效电路较为常用。高频工作情况下,混合 型高频等效电路可表征结电容对电路高频性能的影响。在大信号工作时,必须考虑电子器件的非线性,建立大信号等效电路。
型高频等效电路可表征结电容对电路高频性能的影响。在大信号工作时,必须考虑电子器件的非线性,建立大信号等效电路。
非线性器件的特性常找不到其解析表达式,若要精确地分析非线性电路,只有采用数值分析法。也有一些非线性器件可有合理的近似解析式,如用幂级数或泰勒级数逼近非线性器件特性,也可用分段线性作近似。
分析非线性电路的目的是确定电路的解和解的性质。确定解的局部或全局性质的分析称为定性分析;确定解的数值关系的分析称为定量分析。电路的稳态的定性分析的研究范围是:①平衡点与周期解的存在性和唯一性,解的个数和解的稳定性问题。②非线性现象发生的条件。定量分析的范围是:平衡点的坐标位置、稳态周期解的波形和频谱以及状态变量与电路参数的关系。定性分析可确定电路的全局性质,而定量分析只能得到局部的结果。非线性电路分析理论主要有:①定性分析法中的稳定性理论。各种稳定性判据、考虑扰动的判据、特性方程分析法和李雅普诺夫分析法。②近似解析法。对于二阶电路常用缓变振幅法、奇异扰动法、渐进法和相平面法;对于高阶电路常用等效小参量法。③图解法(拓扑方法)。④数字计算机辅助分析法。⑤用模拟计算机或集成电路进行模拟仿真。
分布参数电路中的电压和电流不仅是时间的函数,还是空间坐标的函数。首先用无限逼近法建立理论模型,将电路(如均匀无耗传输线)设想为许多个无穷小长度元 ,在
,在 范围内参数可集中,每个长度元可抽象为一个集总参数电路,这些集总参数电路级联而成的链形电路就成为传输线的电路模型。显然,只有无穷小长度元
范围内参数可集中,每个长度元可抽象为一个集总参数电路,这些集总参数电路级联而成的链形电路就成为传输线的电路模型。显然,只有无穷小长度元 的个数无限多时,链形电路才能准确地代表传输线。接着是根据模型写方程,方程是参照长度元
的个数无限多时,链形电路才能准确地代表传输线。接着是根据模型写方程,方程是参照长度元 抽象成的集总参数电路,利用基尔霍夫定律和元件约束写出的偏微分方程组。最后是解方程求解答,再根据解答讨论电路(传输线)的性能。分布参数电路作为一个电磁系统还可采用电磁场理论进行分析,虽然严格与精确,但因电磁场方程求解比电路理论方程困难得多,通常不便采用。
抽象成的集总参数电路,利用基尔霍夫定律和元件约束写出的偏微分方程组。最后是解方程求解答,再根据解答讨论电路(传输线)的性能。分布参数电路作为一个电磁系统还可采用电磁场理论进行分析,虽然严格与精确,但因电磁场方程求解比电路理论方程困难得多,通常不便采用。
用时变系数微分方程描述时变电路并求解。这种方程一般求不出解析解,只能作数值分析或求近似解,而且求解过程也很复杂。若时变电路中的元件都是线性元件,描述电路的方程就仍是线性的。具有线性电路的线性性质,叠加定理仍然适用。线性时变电路中的全响应等于其零状态响应与零输入响应之和,而且可由冲激响应和激励的卷积求其零状态响应。
用于分析线性电路的一种方法。特点是利用一个有向图来描述一些变量之间的关系。当这些关系是线性的,则有向图可用来表示一组联立的代数方程。同时方程组的代数变换将与图的变换具有对应的关系,方程组的求解还可根据图的结构,凭直观的方法来进行。另外,信号流图把变量描述为沿着支路流动的“信号”。这些“信号”将被它所经过支路的“特性”所改变,因此这种有向图可把电路的因果关系清楚地在图上表示出来。对于较复杂的信号流图,S.J.梅森公式对所涉及的方程式解答的展开式做出图形上的解释。信号流图分析方法与控制电路系统中最常用的框图表示法非常相似,由电路框图作相应的信号流图也是可用的方法。
用状态变量建立状态方程的分析电路的方法。电路的状态变量具有下述特点:知道这组变量在某一时刻( )的值和施加于此电路在此后(
)的值和施加于此电路在此后( )的输入值,就能完全确定此电路在任何时刻(
)的输入值,就能完全确定此电路在任何时刻( )的性状。同一电路可用多组状态变量中的任一组去描述。选取怎样的一组往往视方便和需要而定。
)的性状。同一电路可用多组状态变量中的任一组去描述。选取怎样的一组往往视方便和需要而定。
状态变量分析法不仅对线性电路适用,也可推广到非线性电路和离散时间电路。连续时间电路的状态方程是一组联立的一阶微分方程。离散时间电路的状态方程是一组联立的一阶差分方程。但状态方程的编写常常比较复杂,有时甚至不可能写成标准形式。对于较为复杂的电路常常采用数值解法。
远大于电路尺寸
时,电路是
与
可比拟时,表征电路特性的参数已不能只用一种常规定义下的物理量来表征,而要用无限多个连续分布的基本电路参数来表征,这种元件称为
的情况下,表征电路特性的参数已不是电压和电流,而是电场强度和磁场强度,这种电路是微波电路。当电路中的信号是连续时间信号时,电路称为模拟电路;当信号是离散时间信号时,电路称为离散时间电路;当信号是二值化(0,1两个状态)信号时,电路是数字电路。特性或参数随时间变化的元件称为时变元件,含时变元件的电路是时变电路;否则分别称为时不变元件和时不变电路。






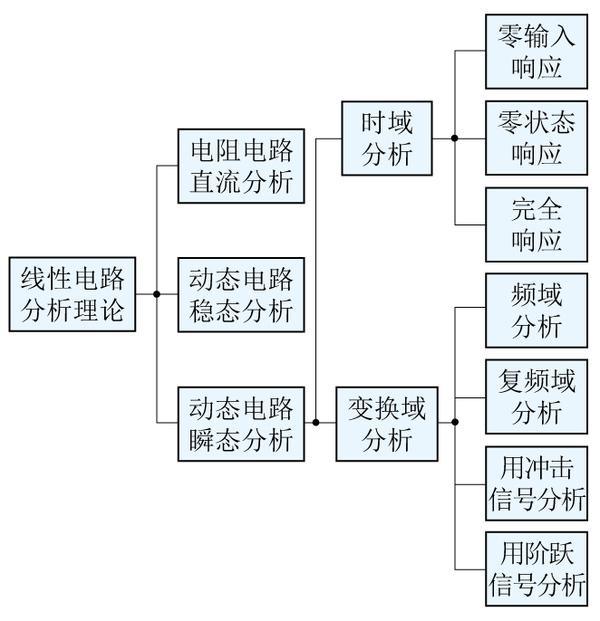 线性电路分析理论
线性电路分析理论

 京公网安备 11010202008139号
京公网安备 11010202008139号
